Communication is not Free

Communication is not free. It takes energy to move data around. In integrated circuits we can move data with electrons on metal wires or, more recently, with photons in waveguides. Photons are a great choice for long-distance communication but they fail for short-distance communication. We cannot compute directly with photons because they do not interact, so we must couple them to stuff that can interact, namely, electrons. It takes energy and space (the circuit) to convert from electrons to photons and back again. We end up with a sort of minimum communication distance, above which optics makes sense but below which it does not. Last I heard this was on the order of 200 µm. The effect of this is that optics does not buy us anything if we do not need to communicate information far before we use it in another computation. But regardless, communication requires time and power.

One common argument against computing architectures which aim to completely circumvent the von Neumann Bottleneck such a quantum computing and physical neural networks, is that Moore’s Law will just keep marching on and —someday— computers will be fast enough to accelerate whatever algorithm, with the implication of “why bother”. We see plots such as the following, where sometime in the near future we will be able to afford a computer with the computational power of all human brains for only $1000:

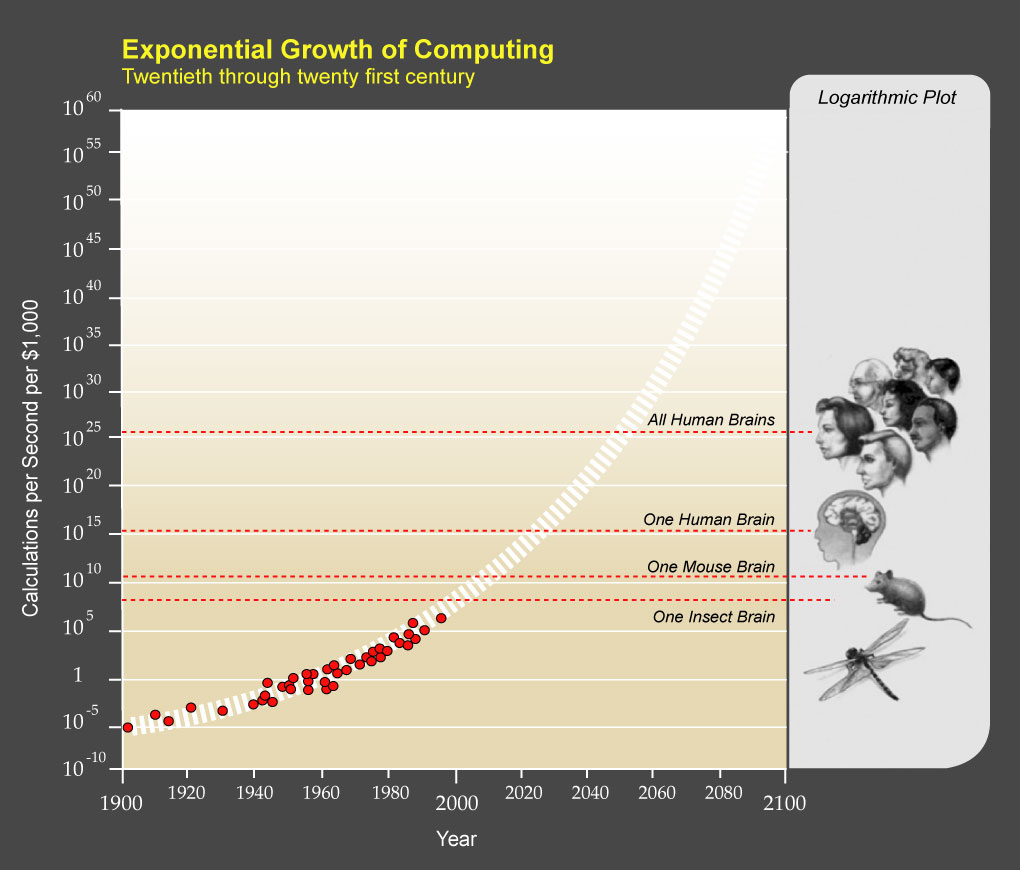
Exponential Growth of Computing by Ray Kurzweil is licensed under CC BY 1.0

While I agree that computers will indeed be very powerful in the near future, and that they will approach and then exceed the capacities of a human brain, I do not agree that they will work exactly like they do today. Something very critical is going to have to happen first. Memory and processor are going to have to merge together, at least for some sub-systems or co-processors.

A Thought Experiment

Let’s perform a thought experiment and calculate a rough estimation of power consumption it would take to simulate a human body on “von Neumann” computer architecture, keeping in mind that the body consumes roughly 100 Watts. This scale is on the low end of the scale between “a brain” and “all human brains”, but could be applied to smaller systems just as well. Whatever the scale, the message is the same: we need to build brains, not simulate them.

Suppose we were to simulate the human body at a moderate fidelity such that each cell of the body was allocated to one processor-memory (CPU+RAM) sub-system, and the distance between memory and processor was d. How much energy would be consumed in just the communication between the memory and processor? Each cell is simulated as a bunch of state variables, and these variables are encoded as bits in the RAM. Through an iterative processes, data moves from RAM to CPU where updates to the state variables are computed and put back in RAM. The more detailed our simulation, the more state variables we need. On one end of the simulation spectrum we could simulate the position, velocity and configuration of every molecule. On the other end we could only encode if it is alive or dead.

This animation from Harvard University gives you a sense of the complex hidden world inside each cell. They are like bustling cities with molecules darting around constantly. If we were to simulate every molecule of a cell, it would end up a more complex version of the Harvard animation:

On the other hand, if we were to use just one state variable, it might look something like Conway’s Game of Life:

Both simulations are interesting, and both could lead to discoveries and insights. Let’s say that each variable is a 32-bit floating point number and we have N variables to update on each ‘time step’ of the simulation. The number of cells in the human body is 50 trillion, give or take a few trillion (source). For each time step, we need to update all of our N state variables. The more accurate our simulation, the faster we must update it. The time scale for biochemical events ranges from a millisecond () for the behavior of discrete cells all the way to femtoseconds () for the vibration of molecular bonds (source). Lets pick a nanosecond (), which is about the timescale of ribosomes–the molecules that transcribe RNA into proteins. In this case the update rate would then be 1 GHz (). Putting this all together we get:

Our theoretical super computer is formed of a huge mesh of locally connected processors, with each processor allocated to one cell. The energy to charge a metal wire goes as (), where C is the capacitance of the wire and V is the voltage. The capacitance of a wire is proportional to length. The longer it is, the more charge it can soak up. A typical dense wire capacitance in CMOS is 0.2 fF/um (source). Putting this together:

Multiplying the equations together, we arrive at our estimate for the energy used in communication as we charge and discharge wires between the CPU and RAM:

Modern CPU and RAM are separated by about 1 centimeter (0.01 m) and the operating voltage is about 1 Volt. If we say we are only going to keep track of 100 variables per cell we would consume 160 trillion watts of energy just in communication. The average human body consumes only 100 watts. But we can do better in the future, perhaps? Our understanding and fabrication capabilities will have improved. We can decrease the distance and lower the voltage. If we lowered the voltage to the thermal voltage to 0.025 Volts and the CPU-memory distance to the diameter of an average cell, d = 10-5 m, it would still consume a hundred million watts.

The above thought experiment and back of the envelop calculations could be applied to even smaller complex systems such as a human brain, a cat brain, or an insect brain. The main take away message is that when you compare biology’s power and space efficiency to a simulated exercise on von Neumann architecture, there is a several orders of magnitude difference. After the numbers are run, it should still be clear that to build such a capable computer is not possible on architectures where processor and memory are separate. This fact is the main motivation to skip to the chase and build a brain instead of simulating (digitally calculating) a brain. This doesn’t apply to relatively simple applications like email clients, web servers and spread sheets, but it does apply to the near and long-term machine learning applications where millions, billions, or trillions of interacting variables need to be continuously read and updated. There simply exists an barrier governed by simple physics: communication requires time and power. The only way around it is to remove the communication — and the only way to do that (so far as we know) is to merge memory and processing like biology has done.

In Nature’s Computers, D=0

You might say “but updating at 1 GHz is too high!“. If you want an accurate simulation of biology, no it is not. But hey–lower it something you think is reasonable, keeping in mind what information you will be losing in the process. 100 variables per cell is certainly on the low end. There are an estimated () protein molecules per liver cell, for example (source) and there are about 5000 synapses per neuron. Perhaps you think 16 bits per variable is more appropriate. By all means, use any assumptions you want. But recognize that your assumptions place real physical bounds on what you can, and can’t, do. Most importantly of all, you should recognize that in all brains, all life, and indeed everywhere in Nature outside of our computers, d is zero.

Based on the known laws of Physics and our insistence on the separation of memory and processing, it is not possible to simulate biology at biological efficiency. Not even close. This is called the “Adaptive Power Problem”, and it is a real bugger of a problem! Why does it matter? Because machine learning systems are large adaptive systems. If we can understand how Nature computes without shuttling information back and forth constantly, we can match and even exceed its efficiency. We could build truly phenomenal learning systems.

Knowm 32X32 W-SDC_Memristor_Crossbar

Knowm Inc’s goal is the creation of learning processors with power efficiencies comparable to and even surpassing biology. To achieve this goal we must make adaption intrinsic to the hardware itself. We must merge memory and processing. Our solution is to define a new type of computing (AHaH Computing) based on a universal adaptive building-block found at most levels of organization on Earth we’ve termed (Knowm’s Synapse). We are ‘bridging the technology stack’ with the KnowmAPI and have designed one possible general purpose learning co-processor chip architecture (Thermodynamic RAM) based on simple RAM coupled to synapses made of memristors.

Thermodynamic RAM, a.k.a. kT-RAM

Learning and Volatility

It goes without saying that the field of machine learning is about learning. Learning, or perhaps more generally adaptation or plasticity, enables a program to adapt based on experience to attain better solutions over time. This is true across all domains of intelligence including perception (feature learning, classification, etc), planning (combinatorial optimizers, classification, etc) and control (motor actuation, reinforcement learning, etc). Take processor A–which can learn continuously, and processor B–which can be programmed into a state but cannot learn. Now make these processors compete in some way. Who wins? The only situation where processor B will be a consistent victor is in an environment that is not changing. If the game is simple and processors A and B are initialized into the Nash Equilibrium then it is likely that processor B will win. This is because processor A will undoubtedly make some mistakes as it attempts to find a better solution, which there is not, and will suffer a lose because of this. However, in the case where the game or environment is complex and always changing–which describes most of the real-world–the learning processor is going to consistently beat the non-learning processor. As the saying goes, “victory goes to the one that makes the second-to-last-mistake”. If you can’t learn from your (or your competitors) mistakes you are doomed in the long run against a competitor that can. What does this have to do with energy and volatility?

Learning in a neuromemristive processor requires modification to the resistance states. For this modification to occur, the energy applied to the memristor must exceed a threshold. (see the generalized MSS Memristor model) The higher this threshold, the more stable (non-volatile) the state but the more energy will be expended in switching, i.e. learning. Reducing the energy cost of adaptation requires a reduction in the switching threshold, but this comes at a cost of increased volatility. This problem is solved in all living systems, as the act of ‘living’ is the act of fighting decay. Stated another way, biological brains are highly volatile systems and are constantly repaired as they are used. For this reason we believe the “end game” solution for AI is one where the memristive processor is built with volatile elements. To be clear, we make a distinction between a synapse that is “volatile” and one that “decays”. A synaptic state that changes if you access it is volatile. A synaptic state that changes on its own without external influence decays. There is a clear trade off:

Non-Volatile: Stability for Free, Adaptation for a Price.
Volatile: Adaptation for Fee, Stability for a Price.

This makes it clear that a processor composed of at least two sub-systems could be a good idea: A volatile system for finding solutions and a non-volatile system for storing them.

What About Quantum Computers?

Some may say “but what about a Universal Quantum Simulator“? On the one hand, quantum computers (QC) are an absolutely amazing and beautiful idea. But as Yogi Berra wisely said “In theory there is no difference between theory and practice. In practice there is.” QC’s rely on the concept of a Qubit. A qubit can exhibit a most remarkable property called quantum entanglement. Entanglement allows quantum particles to become ‘linked’ and behave not as isolated particles but as a system. The problem is that a particle can become linked to anything, like a stray molecule or photon floating around. So long as we can exercise extreme control over the linking, we can exploit the collective to solve problems in truly extraordinary ways. Sounds great right? Absolutely! If it can be built. In the 30 years since physics greats like Richard Feynman starting talking about it, we have yet to realize a practical QC that works better than off-the-shelf hardware. Why is this? Because Nature abhors qubits. It stomps them out as fast as we can make them. Every living cell, every neuron, pretty much every atom and molecule on the planet is constantly interacting with everything around it, and indeed it is the process of this interaction (i.e. decoherence) that define particles in the first place. Using as a base unit of computation a state of matter that Nature clearly abhors is really hard! It is why we end up with machines like this, where we expend tremendous amounts of energy lowering temperatures close to absolute zero. Does this mean a QC is impossible? Of course not. But it has significant practical problems and associated costs that must be overcome and certainly not overlooked.

Summary

While computing architectures separating memory and processor have without a doubt been one of the greatest tools humans have ever built and will continue to be more and more capable, it introduces fundamental limitations in our ability to build large-scale adaptive systems at practical power efficiencies. It is important that we recognize these limitations so that we can overcome them. The first step, as they say, is to admit you have a problem. An adaptive power problem.

The Knowm Technology Stack

The Adaptive Power Problem

The Adaptive Power Solution