A Brief History of Neuromorphic Computing

Sign up for our newsletter for progress updates, product announcements and Knowm news.

Close-up of one of the 4X4X8 crossbar die in a crossbar module

Mimicking Nature’s Computers

How does nature compute? Attempting to answer this question naturally leads one to consider biological nervous systems, although examples of computation abound in other manifestations of life. Some examples include plants [1–5], bacteria [6], protozoan [7], and swarms [8], to name a few. Most attempts to understand biological nervous systems fall along a spectrum. One end of the spectrum attempts to mimic the observed physical properties of nervous systems. These models necessarily contain parameters that must be tuned to match the biophysical and architectural properties of the natural model. Examples of this approach include Boahen’s neuromorphic circuit at Stanford University and their Neurogrid processor [9], the mathematical spiking neuron model of Izhikevich [10] as well as the large scale modeling of Eliasmith [11]. The other end of the spectrum abandons biological mimicry in an attempt to algorithmically solve the problems associated with brains such as perception, planning and control. This is generally referred to as machine learning. Algorithmic examples include support vector maximization [12], k-means clustering [13] and random forests [14].

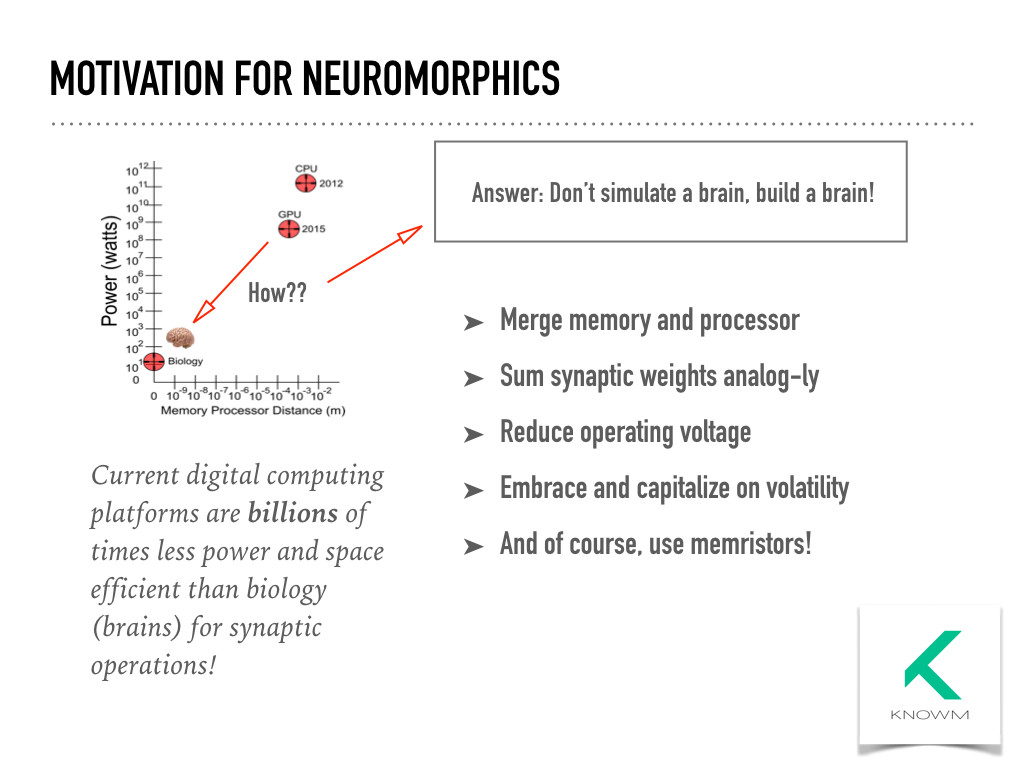
Motivation For Neuromorphics

Many approaches fall somewhere along the spectrum between mimicry and machine learning, such as the CAVIAR [15] and Cognimem [16] neuromorphic processors as well as IBM’s neurosynaptic core [17]. For over a decade, we have been considering an alternative approach outside of the typical spectrum by asking ourselves a simple but important question: How can a brain compute given that it is built of volatile components? Exploring this question has lead us to a formalized theory of “AHaH Computing”, designs for a neuromorphic co-processor called “Thermodynamic RAM” and promising results from our first memristive “Knowm Synapses”. But before we talk about what the future landscape of neuromorphic computing may look like, let’s take a look backwards in time at the groundwork and events that led to the current state of the field.

Standing on the Shoulders of Giants

In 1936, Turing, best known for his pioneering work in computation and his seminal paper ‘On computable numbers’ [18], provided a formal proof that a machine could be constructed to be capable of performing any conceivable mathematical computation if it were representable as an algorithm. This work rapidly evolved to become the computing industry of today. Few people are aware that, in addition to the work leading to the digital computer, Turing anticipated connectionism and neuron-like computing. In his paper ‘Intelligent machinery’ [19], which he wrote in 1948 but was not published until well after his death in 1968, Turing described a machine that consists of artificial neurons connected in any pattern with modifier devices. Modifier devices could be configured to pass or destroy a signal, and the neurons were composed of NAND gates that Turing chose because any other logic function can be created from them.

Image by photoverulam

In 1944, physicist Schrödinger published the book What is Life? based on a series of public lectures delivered at Trinity College in Dublin. Schrödinger asked the question: “How can the events in space and time which take place within the spatial boundary of a living organism be accounted for by physics and chemistry?” He described an aperiodic crystal that predicted the nature of DNA, yet to be discovered, as well as the concept of negentropy being the entropy of a living system that it exports to keep its own entropy low [20].

In 1949, only one year after Turing wrote ‘Intelligent machinery’, synaptic plasticity was proposed as a mechanism for learning and memory by Hebb [21]. Ten years later in 1958 Rosenblatt defined the theoretical basis of connectionism and simulated the perceptron, leading to some initial excitement in the field [22].

In 1953, Barlow discovered neurons in the frog brain fired in response to specific visual stimuli [23]. This was a precursor to the experiments of Hubel and Wiesel who showed in 1959 the existence of neurons in the primary visual cortex of the cat that selectively responds to edges at specific orientations [24]. This led to the theory of receptive fields where cells at one level of organization are formed from inputs from cells in a lower level of organization.

In 1960, Widrow and Hoff developed ADALINE, a physical device that used electrochemical plating of carbon rods to emulate the synaptic elements that they called memistors [25]. Unlike memristors, memistors are three terminal devices, and their conductance between two of the terminals is controlled by the time integral of the current in the third. This work represents the first integration of memristive-like elements with electronic feedback to emulate a learning system.

In 1969, the initial excitement with perceptrons was tampered by the work of Minsky and Papert, who analyzed some of the properties of perceptrons and illustrated how they could not compute the XOR function using only local neurons [26]. The reaction to Minsky and Papert diverted attention away from connection networks until the emergence of a number of new ideas, including Hopfield networks (1982) [27], back propagation of error (1986) [28], adaptive resonance theory (1987) [29], and many other permutations. The wave of excitement in neural networks began to fade as the key problem of generalization versus memorization became better appreciated and the computing revolution took off.

In 1971, Chua postulated on the basis of symmetry arguments the existence of a missing fourth two terminal circuit element called a memristor (memory resistor), where the resistance of the memristor depends on the integral of the input applied to the terminals [30,31].

VLSI pioneer Mead published with Conway the landmark text Introduction to VLSI Systems in 1980 [32]. Mead teamed with John Hopfield and Feynman to study how animal brains compute. This work helped to catalyze the fields of Neural Networks (Hopfield), Neuromorphic Engineering (Mead) and Physics of Computation (Feynman). Mead created the world’s first neural-inspired chips including an artificial retina and cochlea, which was documented in his book Analog VLSI Implementation of Neural Systems published in 1989 [33].

Image by Abode of Chaos

Beinenstock, Cooper and Munro published a theory of synaptic modification in 1982 [34]. Now known as the BCM plasticity rule, this theory attempts to account for experiments measuring the selectivity of neurons in primary sensory cortex and its dependency on neuronal input. When presented with data from natural images, the BCM rule converges to selective oriented receptive fields. This provides compelling evidence that the same mechanisms are at work in cortex, as validated by the experiments of Hubel and Wiesel. In 1989 Barlow reasoned that such selective response should emerge from an unsupervised learning algorithm that attempts to find a factorial code of independent features [35]. Bell and Sejnowski extended this work in 1997 to show that the independent components of natural scenes are edge filters [36]. This provided a concrete mathematical statement on neural plasticity: Neurons modify their synaptic weight to extract independent components. Building a mathematical foundation of neural plasticity, Oja and collaborators derived a number of plasticity rules by specifying statistical properties of the neuron’s output distribution as objective functions. This lead to the principle of independent component analysis (ICA) [37,38].

At roughly the same time, the theory of support vector maximization emerged from earlier work on statistical learning theory from Vapnik and Chervonenkis and has become a generally accepted solution to the generalization versus memorization problem in classifiers [12,39].

In 2004, Nugent et al. showed how the AHAH plasticity rule is derived via the minimization of a kurtosis objective function and used as the basis of self-organized fault tolerance in support vector machine network classifiers. Thus, the connection that margin maximization coincides with independent component analysis and neural plasticity was demonstrated [40,41]. In 2006, Nugent first detailed how to implement the AHaH plasticity rule in memristive circuitry and demonstrated that the AHaH attractor states can be used to configure a universal reconfigurable logic gate [42–44].

In 2008, HP Laboratories announced the production of Chua’s postulated electronic device, the memristor [45] and explored their use as synapses in neuromorphic circuits [46]. Several memristive devices demonstrating the tell-tale hysteresis loops were previously reported by this time, predating HP Laboratories [47–51], but they were not described as memristors. In the same year, Hylton and Nugent launched the Systems of Neuromorphic Adaptive Plastic Scalable Electronics (SyNAPSE) program with the goal of demonstrating large scale adaptive learning in integrated memristive electronics at biological scale and power. Since 2008 there has been an explosion of worldwide interest in memristive devices [52–56] device models [57–62], their connection to biological synapses [63–69], and use in alternative computing architectures [70–81].

In early 2014, we published AHaH Computing — From Metastable Switches to Attractors to Machine Learning, a formal introduction to a new approach to computing we call “AHaH Computing” where, unlike traditional computers, memory and processing are combined. The idea is based on the attractor dynamics of volatile dissipative electronics inspired by biological systems, presenting an attractive alternative architecture that is able to adapt, self-repair, and learn from interactions with the environment. We demonstrated high level machine learning functions including unsupervised clustering, supervised and unsupervised classification, complex signal prediction, unsupervised robotic actuation and combinatorial optimization. Later that same year, we published Thermodynamic RAM Technology Stack and Cortical Computing with Thermodynamic-RAM, outlining a design and full stack integration including the kT-RAM instruction set and the Knowm API for putting AHaH-based neuromorphic learning co-processors into existing computer platforms.

kT-RAM

In late 2014, IBM announced their “spiking-neuron integrated circuit” called TrueNorth, circumventing the von-Neumann-architecture bottlenecks, boasting a power consumption of 70 mW, about 1/10,000 th the power density of conventional microprocessors. It is however not currently capable of on-chip learning or adaptation.

What About Quantum Computers?

Quantum computers are an absolutely amazing and beautiful idea. But as Yogi Berra wisely said “In theory there is no difference between theory and practice. In practice there is.” QCs rely on the concept of a Qubit. A qubit can exhibit a most remarkable property called quantum entanglement. Entanglement allows quantum particles to become ‘linked’ and behave not as isolated particles but as a system. The problem is that a particle can become linked to anything, like a stray molecule or photon floating around. So long as we can exercise extreme control over the linking, we can exploit the collective to solve problems in truly extraordinary ways. Sounds great right? Absolutely! If it can be built. In the 30 years since physics greats like Richard Feynman starting talking about it, we have yet to realize a practical QC that works better than off-the-shelf hardware. Why is this? Because Nature abhors qubits. It stomps them out as fast as we can make them. Every living cell, every neuron, pretty much every atom and molecule on the planet is constantly interacting with everything around it, and indeed it is the process of this interaction (i.e. decoherence) that define particles in the first place. Using as a base unit of computation a state of matter that Nature clearly abhors is really hard! It is why we end up with machines like this, where we expend tremendous amounts of energy lowering temperatures close to absolute zero. Does this mean a QC is impossible? Of course not. But it has significant practical problems and associated costs that must be overcome and certainly not overlooked.

In a Google Tech Talk, Seth Lloyd says that quantum computing is inherently difficult to understand.

“It’s strange, it’s weird, and it goes against your intuitions.” –Seth Lloyd

So will a technology that is hard to understand and use (also assuming it will even deliver on its promises) gain wide adoption if only a few people, the people who built it, know how to use it? Wouldn’t a technology that is “straight-forward, familiar and intuitive” be better? We’re not saying that quantum computing should not be pursued, just that people should keep in mind all the practical considerations when evaluating an AI technology.

Looking Ahead

The race is definitely on to build and commercialize the world’s first truly neuromorphic chips and open up a door to unimaginable possibilities in low-power, low-volume and high-speed machine learning applications. We’re obviously biased toward our own path and believe that our methods and results so far stand their ground and provide a solid foundation to build upon. Alex’s original idea and inspiration over a decade ago was to “reevaluate our preconceptions of how computing works and build a new type of processor that physically adapts and learns on its own”. In a nervous system (and all other natural systems), the processor and memory are the same machinery. The distance between processor and memory is zero. Whereas modern chips must maintain absolute control over internal states (ones and zeros), Nature’s computers are volatile – the components are analog, their states decay, and they heal and build themselves continuously. Driven by the second law of thermodynamics, matter spontaneously configures itself to optimally dissipate the flow of energy. The challenge remaining was to figure out how to recreate this phenomenon on a chip and understand it sufficiently to interface with existing hardware and solve real-world machine learning problems. Years of work designing various chip architectures and validating capabilities lead to the specification of Thermodynamic RAM or kT-RAM for short, a co-processor that can be plugged into existing hardware platforms to accelerate machine learning tasks. Validated capabilities of kT-RAM include unsupervised clustering, supervised and unsupervised classification, complex signal prediction, anomaly detection, unsupervised robotic actuation and combinatorial optimization of procedures – all key capabilities of biological nervous systems and modern machine learning algorithms with real world application.

To learn more about the theory of AHaH computing and how memristive+CMOS circuits can be turned into self-learning computer architecture using the AHaH plasticity, dive into our open-access PLOS One paper: AHaH Computing–From Metastable Switches to Attractors to Machine Learning. Alternatively, check out our Technology page or head on over to knowm.org/learn!

Neuromorphic Computing Trends

If you’re still not convinced, you don’t have to take our word for it anymore! The new White House grand challenge for future computing has just been announced and it fits exactly the motivations for developing a new type of computer.

Neuromorphics Grand Challenge

Similar challenges are appearing in Europe and other parts of the world as well. The first call for proposals just came out and is co-sponsored by SRC and the NSF, and note the two main points it highlights:

1. severely limited by physics of managing data
2. constrained by physical and economical limits

This says, what we’ve been saying for a long time, you need to build a brain, where the distance is zero between memory and processor, and stop trying to simulate a brain on a digital platform!

References

1. Grime JP, Crick JC, Rincon JE (1985) The ecological significance of plasticity. In: Proc. 1985 Symposia of the Society for Experimental Biology. volume 40, pp. 5–29.
2. Desbiez MO, Kergosien Y, Champagnat P, Thellier M (1984) Memorization and delayed expression of regulatory messages in plants. Planta 160: 392–399.
3. Aphalo PJ, Ballar ́e CL (1995) On the importance of information-acquiring systems in plant–plant interactions. Functional Ecology 9: 5–14.
4. Falik O, Reides P, Gersani M, Novoplansky A (2003) Self/non-self discrimination in roots. Journal of Ecology 91: 525–531.
5. Scialdone A, Mugford ST, Feike D, Skeffington A, Borrill P, et al. (2013) Arabidopsis plants perform arithmetic division to prevent starvation at night. eLife 2 doi: 10.7554/eLife.00669.
6. von Bodman SB, Bauer WD, Coplin DL (2003) Quorum sensing in plant-pathogenic bacteria. Annual Review of Phytopathology 41: 455–482.
7. Nakagaki T, Yamada H, T ́oth A ́ (2000) Intelligence: Maze-solving by an amoeboid organism. Nature 407: 470–470.
8. Bonabeau E, Dorigo M, Theraulaz G (1999) Swarm Intelligence: from Natural to Artificial Systems, volume 4. Oxford University press New York.
9. Choudhary S, Sloan S, Fok S, Neckar A, Trautmann E, et al. (2012) Silicon neurons that compute. In: Artificial Neural Networks and Machine Learning – ICANN 2012, Springer Berlin Heidelberg, volume 7552 of Lecture Notes in Computer Science. pp. 121-128.
10. Izhikevich EM (2003) Simple model of spiking neurons. IEEE Transactions on Neural Networks 14: 1569–1572.
11. Eliasmith C, Stewart TC, Choo X, Bekolay T, DeWolf T, et al. (2012) A large scale model of the functioning brain. Science 338: 1202–1205.
12. Boser BE, Guyon IM, Vapnik VN (1992) A training algorithm for optimal margin classifiers. In: Proc. 1992 ACM 5th Annual Workshop on Computational Learning Theory. pp. 144–152.
13. MacQueen J (1967) Some methods for classification and analysis of multivariate observations. In: Proc. 1967 5th Berkeley Symposium on Mathematical Statistics and Probability. 281-297, p. 14.
14. Breiman L (2001) Random forests. Machine Learning 45: 5–32.
15. Serrano-Gotarredona R, Oster M, Lichtsteiner P, Linares-Barranco A, Paz-Vicente R, et al. (2009) CAVIAR: A 45k neuron, 5M synapse, 12G connects/s AER hardware sensory–processing–learning– actuating system for high-speed visual object recognition and tracking. IEEE Transactions on Neural Networks 20: 1417–1438.
16. Sardar S, Tewari G, Babu KA (2011) A hardware/software co-design model for face recognition using cognimem neural network chip. In: Proc. 2011 IEEE International Conference on Image Information Processing (ICIIP). pp. 1–6.
17. Arthur JV, Merolla PA, Akopyan F, Alvarez R, Cassidy A, et al. (2012) Building block of a programmable neuromorphic substrate: A digital neurosynaptic core. In: Proc. 2012 IEEE Inter- national Joint Conference on Neural Networks (IJCNN). pp. 1–8.
18. Turing AM (1936) On computable numbers, with an application to the entscheidungsproblem. Proceedings of the London Mathematical Society 42: 230–265.
19. Turing A (1948) Intelligent machinery. Report, National Physical Laboratory.
20. Schrodinger E (1992) What is Life?: With Mind and Matter and Autobiographical Sketches. Cambridge University Press.
21. Hebb DO (2002) The Organization of Behavior: A Neuropsychological Theory. Psychology Press.
22. Rosenblatt F (1958) The perceptron: a probabilistic model for information storage and organization in the brain. Psychological Review 65: 386.
23. Barlow HB (1953) Summation and inhibition in the frog’s retina. The Journal of Physiology 119: 69–88.
24. Hubel DH, Wiesel TN (1959) Receptive fields of single neurones in the cat’s striate cortex. The Journal of Physiology 148: 574–591.
25. Widrow B (1987) The original adaptive neural net broom-balancer. In: Proc. 1987 IEEE Interna- tional Symposium on Circuits and Systems. volume 2, pp. 351–357.
26. Minsky M, Seymour P (1969) Perceptrons. MIT press.
27. Hopfield JJ (1982) Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences of the United States of America 79: 2554–2558.
28. Rumelhart DE, Hinton GE, Williams RJ (1986) Learning representations by back-propagating errors. Nature 323: 533–536.
29. Grossberg S (1987) Competitive learning: from interactive activation to adaptive resonance. Cog- nitive Science 11: 23–63.
30. Chua L (1971) Memristor—the missing circuit element. IEEE Transactions on Circuit Theory 18: 507–519.
31. Chua LO, Kang SM (1976) Memristive devices and systems. Proceedings of the IEEE 64: 209–223.
32. Mead C, Conway L (1980) Introduction to VLSI Systems. Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc.
33. Mead C, Ismail M (1989) Analog VLSI Implementation of Neural Systems. Springer.
34. Bienenstock EL, Cooper LN, Munro PW (1982) Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. The Journal of Neuroscience 2: 32–48.
35. Barlow HB (1989) Unsupervised learning. Neural Computation 1: 295–311.
36. Bell AJ, Sejnowski TJ (1997) The independent components of natural scenes are edge filters. Vision Research 37: 3327–3338.
37. Hyvarinen A, Oja E (1997) A fast fixed-point algorithm for independent component analysis. Neural Computation 9: 1483–1492.
38. Comon P (1994) Independent component analysis, a new concept? Signal Processing 36: 287–314.
39. Scholkopf , Simard P, Vapnik V, Smola AJ (1997) Improving the accuracy and speed of support vector machines. Advances in Neural Information Processing Systems 9: 375–381.
40. Nugent A, Kenyon G, Porter R (2004) Unsupervised adaptation to improve fault tolerance of neural network classifiers. In: Proc. 2004 IEEE NASA/DoD Conference on Evolvable Hardware. pp. 146–149.
41. Nugent MA, Porter R, Kenyon GT (2008) Reliable computing with unreliable components: using separable environments to stabilize long-term information storage. Physica D: Nonlinear Phenom- ena 237: 1196–1206.
42. Nugent A (2008). Plasticity-induced self organizing nanotechnology for the extraction of indepen- dent components from a data stream. US Patent 7,409,375.
43. Nugent A (2008). Universal logic gate utilizing nanotechnology. US Patent 7,420,396.
44. Nugent A (2009). Methodology for the configuration and repair of unreliable switching elements. US Patent 7,599,895.
45. YangJJ,PickettMD,LiX,OhlbergDA,StewartDR,etal.(2008)Memristiveswitchingmechanism for metal/oxide/metal nanodevices. Nature Nanotechnology 3: 429–433.
46. Snider GS (2008) Spike-timing-dependent learning in memristive nanodevices. In: Proc. 2008 IEEE International Symposium on Nanoscale Architectures (NANOARCH). pp. 85–92.
47. Stewart DR, Ohlberg DAA, Beck PA, Chen Y, Williams RS, et al. (2004) Molecule-independent electrical switching in Pt/organic monolayer/Ti devices. Nano Letters 4: 133-136.
48. Kozicki MN, Gopalan C, Balakrishnan M, Mitkova M (2006) A low-power nonvolatile switching element based on copper-tungsten oxide solid electrolyte. IEEE Transactions on Nanotechnology 5: 535–544.
49. Szot K, Speier W, Bihlmayer G, Waser R (2006) Switching the electrical resistance of individual dislocations in single-crystalline SrTiO3. Nature Materials 5: 312–320.
50. Dong R, Lee D, Xiang W, Oh S, Seong D, et al. (2007) Reproducible hysteresis and resistive switching in metal-CuxO-metal heterostructures. Applied Physics Letters 90: 042107.
51. Tsubouchi K, Ohkubo I, Kumigashira H, Oshima M, Matsumoto Y, et al. (2007) High-throughput characterization of metal electrode performance for electric-field-induced resistance switching in metal/Pr0.7Ca0.3MnO3/metal structures. Advanced Materials 19: 1711–1713.
52. ObleaAS,TimilsinaA,MooreD,CampbellKA(2010)Silverchalcogenidebasedmemristordevices. In: Proc. 2010 IEEE International Joint Conference on Neural Networks (IJCNN). pp. 1–3.
53. Yang Y, Sheridan P, Lu W (2012) Complementary resistive switching in tantalum oxide-based resistive memory devices. Applied Physics Letters 100: 203112.
54. Valov I, Kozicki MN (2013) Cation-based resistance change memory. Journal of Physics D: Applied Physics 46: 074005.
55. Hasegawa T, Nayak A, Ohno T, Terabe K, Tsuruoka T, et al. (2011) Memristive operations demon- strated by gap-type atomic switches. Applied Physics A 102: 811–815.
56. Jackson BL, Rajendran B, Corrado GS, Breitwisch M, Burr GW, et al. (2013) Nanoscale electronic synapses using phase change devices. ACM Journal on Emerging Technologies in Computing Systems (JETC) 9: 12.
57. Choi S, Ambrogio S, Balatti S, Nardi F, Ielmini D (2012) Resistance drift model for conductive- bridge (CB) RAM by filament surface relaxation. In: Proc. 2012 IEEE 4th International Memory Workshop (IMW). pp. 1–4.
58. Pino RE, Bohl JW, McDonald N, Wysocki B, Rozwood P, et al. (2010) Compact method for mod- eling and simulation of memristor devices: ion conductor chalcogenide-based memristor devices. In: Proc. 2010 IEEE/ACM International Symposium on Nanoscale Architectures (NANOARCH). pp. 1–
59. Menzel S, Bottger U, Waser R (2012) Simulation of multilevel switching in electrochemical metal- lization memory cells. Journal of Applied Physics 111: 014501.
60. Chang T, Jo SH, Kim KH, Sheridan P, Gaba S, et al. (2011) Synaptic behaviors and modeling of a metal oxide memristive device. Applied Physics A 102: 857–863.
61. Sheridan P, Kim KH, Gaba S, Chang T, Chen L, et al. (2011) Device and SPICE modeling of RRAM devices. Nanoscale 3: 3833–3840.
62. Biolek D, Biolek Z, Biolkova V (2009) SPICE modeling of memristive, memcapacitative and me- minductive systems. In: Proc. 2009 IEEE European Conference on Circuit Theory and Design (ECCTD). pp. 249–252.
63. Chang T, Jo SH, Lu W (2011) Short-term memory to long-term memory transition in a nanoscale memristor. ACS Nano 5: 7669–7676.
64. Merrikh-Bayat F, Shouraki SB, Afrakoti IEP (2010) Bottleneck of using single memristor as a synapse and its solution. preprint arXiv: cs.NE/1008.3450.
65. Jo SH, Chang T, Ebong I, Bhadviya BB, Mazumder P, et al. (2010) Nanoscale memristor device as synapse in neuromorphic systems. Nano Letters 10: 1297–1301.
66. Hasegawa T, Ohno T, Terabe K, Tsuruoka T, Nakayama T, et al. (2010) Learning abilities achieved by a single solid-state atomic switch. Advanced Materials 22: 1831–1834.
67. Li Y, Zhong Y, Xu L, Zhang J, Xu X, et al. (2013) Ultrafast synaptic events in a chalcogenide memristor. Scientific Reports 3 doi:10.1038/srep01619.
68. Merrikh-Bayat F, Shouraki SB (2011) Memristor-based circuits for performing basic arithmetic operations. Procedia Computer Science 3: 128–132.
69. Merrikh-Bayat F, Shouraki SB (2013) Memristive neuro-fuzzy system. IEEE Transactions on Cybernetics 43: 269-285.
70. Morabito FC, Andreou AG, Chicca E (2013) Neuromorphic engineering: from neural systems to brain-like engineered systems. Neural Networks 45: 1–3.
71. Klimo M, Such O (2011) Memristors can implement fuzzy logic. preprint arXiv cs.ET/1110.2074.
72. Klimo M, Such O (2012) Fuzzy computer architecture based on memristor circuits. In: Proc. 2012 4th International Conference on Future Computational Technologies and Applications. pp. 84–87.
73. Kavehei O, Al-Sarawi S, Cho KR, Eshraghian K, Abbott D (2012) An analytical approach for memristive nanoarchitectures. IEEE Transactions on Nanotechnology 11: 374–385.
74. Rosezin R, Linn E, Nielen L, Kugeler C, Bruchhaus R, et al. (2011) Integrated complementary resistive switches for passive high-density nanocrossbar arrays. IEEE Electron Device Letters 32: 191–193.
75. Kim KH, Gaba S, Wheeler D, Cruz-Albrecht JM, Hussain T, et al. (2011) A functional hybrid memristor crossbar-array/CMOS system for data storage and neuromorphic applications. Nano Letters 12: 389–395.
76. Jo SH, Kim KH, Lu W (2009) High-density crossbar arrays based on a Si memristive system. Nano Letters 9: 870–874.
77. Xia Q, Robinett W, Cumbie MW, Banerjee N, Cardinali TJ, et al. (2009) Memristor-CMOS hybrid integrated circuits for reconfigurable logic. Nano Letters 9: 3640–3645.
78. Strukov DB, Stewart DR, Borghetti J, Li X, Pickett M, et al. (2010) Hybrid CMOS/memristor circuits. In: Proc. 2010 IEEE International Symposium on Circuits and Systems (ISCAS). pp. 1967–1970.
79. Snider G (2011) Instar and outstar learning with memristive nanodevices. Nanotechnology 22: 015201.
80. Thomas A (2013) Memristor-based neural networks. Journal of Physics D: Applied Physics 46: 093001.
81. Indiveri G, Linares-Barranco B, Legenstein R, Deligeorgis G, Prodromakis T (2013) Integra- tion of nanoscale memristor synapses in neuromorphic computing architectures. preprint arXiv cs.ET/1302.7007.