AHaH Computing Silent Intro from Knowm on Vimeo.

AHaH Computing in a Nutshell

A series of short introductory presentations on AHaH Computing, starting with memristors and motivations for AHaH Computing. Click Here

AHaH Computing–From Metastable Switches to Attractors to Machine Learning

Peer reviewed open-access manuscript. Click Here

The Next Step in Computing: Neuromemristive Processors

Machine learning (ML) systems are composed of (usually large) numbers of adaptive weights. The goal of ML is to adapt the values of these weights based on exposure to data to optimize a function. This foundational objective of ML creates friction with modern methods of computing because every adaptation event must reduce to a communication procedure between memory and processing separated by a distance. The power required to simulate adaptive weights grows impractically large as the number of weights increases owing to the tremendous energy consumed shuttling information back and forth. This is commonly knowm as the von Neumann Bottleneck and leads to the The Adaptive Power Problem.

Knowm 1X16 Memristor Array Chip (Front)

If current computing methods give us the (remarkable) ability to simulate any possible interaction or “adaptation”, why pursue any other method of computing? The answer is simple: Energy. Nature does not separate memory and processing. Rather, the act of memory access is the act of computing is the act of learning. As the memory processing distance goes to zero, as the case in Nature and proposed neuromemristive architectures, the power efficiency improves by orders of magnitude compared to von Neumann computers. If we want ML systems that are as powerful and efficient as Nature’s examples, then we must create a new type of hardware that is intrinsically adaptive. One could think of it as “Soft-Hardware”.

Neurobiological research has unearthed dozens of plasticity methods, and they all appear to be important to brain function. The more one digs into the literature, the more complex and confusing it becomes. How do we choose a method, or combination of methods, to include in our soft-hardware? It is often said that problems cannot be solved at the same level of thinking that created them. When we step back a level from the brain and we look at all of Nature, we find a viable solution. It is all around us in both biological and non-biological form. The solution is simple, ubiquitous, and it is provably universal.

Taking a Hint from Nature

We find it in rivers, trees, lighting and fungus, but we also find it deep within us. The air that we breath is coupled to our blood through thousands of bifurcating flow channels that form our lungs. Our brain is coupled to our blood through thousands of bifurcating flow channels that form our circulatory system. The neurons in our brains are coupled to each other through thousands of bifurcating flow channels that form our axons and dendrites. Notice a pattern? It is in rivers, lightening, plants, mycelium networks, and even multi-cellular bacteria.

Image by snowpeak

At all scales of organization we see the same patterns built from the same building block. Evolution itself is a bifurcating energy-dissipating structure that spreads out in time like a lightning bolt. All of these processes are fundamentally related and can be described as free energy dissipating itself through adaptive containers or, more generally, as energy dissipation pathways competing for conducting resources. We call this mechanism or process Anti-Hebbian and Hebbian (AHaH) plasticity. It is computationally universal, but perhaps more importantly, it leads to general-purpose solutions in machine learning.

AHaH!

So how does nature compute? A brain, like all living systems, is a far-from-equilibrium energy dissipating structure that constantly builds and repairs itself. We can shift the standard question from “how do brains compute?” or “what is the algorithm of the brain?” to a more fundamental question of “how do brains build and repair themselves as dissipative attractor-based structures?” Just as a ball will roll into a depression, an attractor-based system will fall into its attractor states. Perturbations (damage) will be fixed as the system reconverges to its attractor state. As an example, if we cut ourselves we heal. To bestow this property on our computing technology we must find a way to represent our computing structures as attractors.

In our PLoS One paper we detailed how the attractor points of a plasticity rule we call Anti-Hebbian and Hebbian (AHaH) plasticity are computationally complete logic functions as well as building blocks for machine learning functions. We further showed that AHaH plasticity can be attained from simple memristive circuitry attempting to maximize circuit power dissipation in accordance with ideas in non-equilibrium Thermodynamics. Our goal was to lay a foundation for a new type of practical computing based on the configuration and repair of volatile switching elements. We have traversed the large gap from volatile memristive devices to demonstrations of computational universality and machine learning. In short, it has been demonstrated that:

AHaH plasticity emerges from the interaction of volatile competing energy dissipating pathways.
AHaH plasticity leads to attractor states that can be used for universal computation and advanced machine learning
Neural nodes operating AHaH plasticity can be constructed from simple memristive circuits.

On the Origins of Algorithms and the 4th Law of Thermodynamics

Turing spent the last two years of his life working on mathematical biology and published a paper titled “The chemical basis of morphogenesis” in 1952 [1]. Turing was likely struggling with the concept that algorithms represent structure, brains and life in general are clearly capable of creating such structure, and brains are ultimately a biological chemical process that emerge from chemical homogeneity. How does complex spatial-temporal structure such as an algorithm emerge from the interaction of a homogeneous collection of units?

Image by christopher_brown

Answering this question in a physical sense leads one straight into the controversial 4th law of Thermodynamics. The 4th law is attempting to answer a simple question with profound consequences if a solution is found: If the 2nd law says everything tends towards disorder, why does essentially everything we see in the Universe contradict this? At almost every scale of the Universe we see self-organized structures, from black holes to stars, planets and suns to our own earth, the life that abounds on it and in particular the brain. Non-biological systems such as Benard convection cells [2], tornadoes, lightning and rivers, to name just a few, show us that matter does not tend toward disorder in practice but rather does quite the opposite. In another example, metallic spheres in a non-conducting liquid medium exposed to an electric field will self-organize into fractal dendritic trees [3].

One line of argument is that ordered structures create entropy faster than disordered structures do and self-organizing dissipative systems are the result of out of equilibrium thermodynamics. In other words, there may not actually be a distinct 4th law, and all observed order may actually result from dynamics yet to be unraveled mathematically from the 2nd law. Unfortunately this argument does not leave us with an understanding sufficient to allow us to exploit the phenomena in our technology. In this light, our work with AHaH attractor states may provide a clue as to the nature of the 4th law in so much as it lets us construct useful self-organizing and adaptive computing systems.

One particularly clear and falsifiable formulation of the 4th law comes from Swenson in 1989:

“A system will select the path or assembly of paths out of available paths that minimizes the potential or maximizes the entropy at the fastest rate given the constraints [4].” –Rod Swenson

Others have converged on similar thoughts. For example, Bejan postulated in 1996 that:

“For a finite-size system to persist in time (to live), it must evolve in such a way that it provides easier access to the imposed currents that flow through it [5].” — Adrian Bejan

Bejan’s formulation seems intuitively correct when one looks at nature, although it has faced criticism that it is a bit too vague about what particles are flowing and does not describe physically how exactly a system will provide easier access to its currents–only that it will. We observe that in many cases the particle is either directly a carrier of free energy dissipation or else it gates access, like a key to a lock, to free energy dissipation of the units in the collective. These particles are not hard to spot. Examples include water in plants, ATP in cells, blood in bodies, neurotrophins in brains, and money in economies.

Image by feral arts

More recently, Jorgensen and Svirezhev have put forward the maximum power principle [6] and Schneider and Sagan have elaborated on the simple idea that “nature abhors a gradient” [7]. Others have put forward similar notions much earlier. Morowitz claimed in 1968 that the flow of energy from a source to a sink will cause at least one cycle in the system [7] and Lotka postulated the principle of maximum energy flux in 1922 [8].

The Container Adapts

Hatsopoulos and Keenan’s law of stable equilibrium [9] states that:

“When an isolated system performs a process, after the removal of a series of internal constraints, it will always reach a unique state of equilibrium; this state of equilibrium is independent of the order in which the constraints are removed.”

The idea is that a system erases any knowledge about how it arrived in equilibrium. Schneider and Sagan state this observation in their book Into the Cool: Energy Flow, Thermodynamics, and Life [7] by claiming: “These principles of erasure of the path, or past, as work is produced on the way to equilibrium hold for a broad class of thermodynamic systems.” This principle has been illustrated by connected rooms, where doors between the rooms are opened according to a particular sequence, and only one room is pressurized at the start. The end state is the same regardless of the path taken to get there. The problem with this analysis is that it relies on an external agent: the door opener.

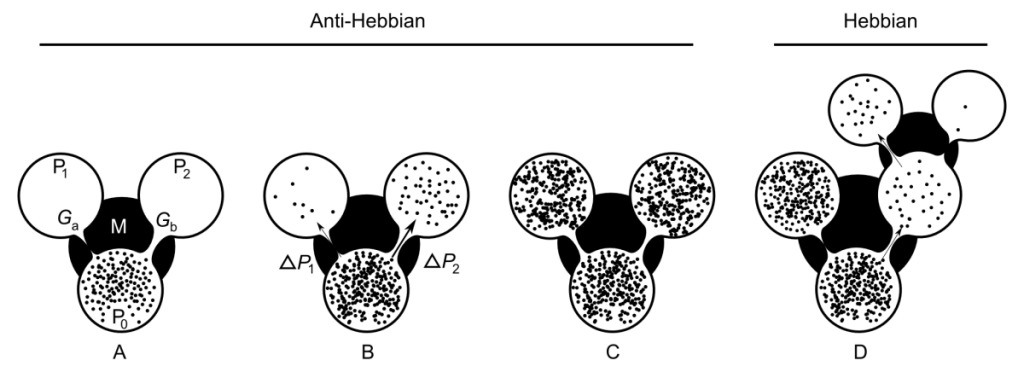
AHaH Computing

Figure 1 AHaH process. A) A first replenished pressurized container $P_0$ is allowed to diffuse into two non-pressurized empty containers $P_1$ and $P_2$ though a region of matter M. B) The gradient ∆P2 reduces faster than the gradient ∆P1 due to the conductance differential. C) This causes $G_a$ to grow more than $G_b$ , reducing the conductance differential and leading to anti-Hebbian learning. D) The first detectable signal (work) is available at $P_2$ owing to the differential that favors it. As a response to this signal, events may transpire in the environment that open up new pathways to particle dissipation. The initial conductance differential is reinforced leading to Hebbian learning.

We may reformulate this idea in the light of an adaptive container, as shown in the Figure 1. A first replenished pressurized container $P_0$ is allowed to diffuse into two non-pressurized empty containers $P_1$ and $P_2$ though a region of matter M. Let us presume that the initial fluid conductance $G_a$ between $P_0$ and $P_1$ is less than $G_b$ . Competition for limited resources within the matter (conservation of matter) enforces the condition that the sum of conductances is constant:

$G_{\rm a}+G_{\rm b}=k$

Now we ask how the container adapts as the system attempts to come to equilibrium. If it is the gradient that is driving the change in the conductance, then it becomes immediately clear that the container will adapt in such a way as to erase any initial differential conductance:

$\Delta G = \lambda \Delta P\Delta t$

The gradient ∆P2 will reduce faster than the gradient ∆P1 and $G_a$ will grow more than $G_b$ . When the system comes to equilibrium we will find that the conductance differential, $G_a$ − $G_b$ has been reduced.

The sudden pressurization of $P_2$ may have an effect on the environment. In the moments right after the flow sets up, the first detectable signal (work) will be available at $P_2$ owing to the differential that favors it. As a response to this signal, any number of events could transpire in the environment that open up new pathways to particle dissipation. The initial conductance differential will be reinforced as the system rushes to equalize the gradient in this newly discovered space. Due to conservation of adaptive resources (first equation), an increase in $G_b$ will require a drop in $G_a$ , and vice versa. The result is that as ∆P1 → 0, $G_a$ → 0, $G_b$ → k and the system selects one pathway over another. The process illustrated in Figure 1 creates structure so long as new sinks are constantly found and a constant particle source is available.

Anti-Hebbian and Hebbian (AHaH) Plasticity

The thermodynamic process outlined above can be understood more broadly as: (1) particles spread out along all available pathways through the environment and in doing so erode any differentials that favor one branch over the other, and (2) pathways that lead to dissipation (the flow of the particles) are stabilized. Let us first identify a synaptic weight, w, as the differential conductance formed from two energy dissipating pathways:

$w = G_{\rm a}-G_{\rm b}$

We can now see that the synaptic weight possess state information. If $G_a$ > $G_b$ the synapse is positive and if $G_a$ < $G_b$ then it is negative. With this in mind we can explicitly define AHaH learning:

Anti-Hebbian (erase the path): Any modification to the synaptic weight that reduces the probability that the synaptic state will remain the same upon subsequent measurement.
Hebbian (select the path): Any modification to the synaptic weight that increases the probability that the synaptic state will remain the same upon subsequent measurement.

Our use of Hebbian learning follows a standard mathematical generalization of Hebb’s famous postulate:

“When an axon of cell A is near enough to excite B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing B, is increased [10].” –Donald Hebb

Hebbian learning can be represented mathematically as ∆w ∝ xy, where x and y are the activities of the pre- and post-synaptic neurons and ∆w is the change to the synaptic weight between them. Anti- Hebbian learning is the negative of Hebbian: ∆w ∝ −xy. Notice that intrinsic to this mathematical definition is the notion of state. The pre- and post-synaptic activities as well as the weight may be positive or negative. We achieve the notion of state in our physical circuits via differential conductances.

Linear Neuron Model

To begin our mapping of AHaH plasticity to computing and machine learning systems we use a standard linear neuron model. The choice of a linear neuron is motivated by the fact that they are ubiquitous in machine learning and also because it is easy to achieve the linear sum function in a physical circuit, since currents naturally sum.

The inputs $x_i$ in a linear model are the outputs from other neurons or spike encoders (to be discussed). The weights $w_i$ are the strength of the inputs. The larger $w_i$ , the more $x_i$ affects the neuron’s output.

Each input $x_i$ is multiplied by a corresponding weight $w_i$ and these values, combined with the bias b, are summed together to form the output y:

$y = b+\sum\limits_{i = 0}^N {{x_i}{w_i}}$

The weights and bias change according to AHaH plasticity, which we further detail in the sections that follow. The AHaH rule acts to maximize the margin between positive and negative classes. In what follows, AHaH nodes refer to linear neurons implementing the AHaH plasticity rule.

AHaH Attractors Extract Independent Components

What we desire is a mechanism to extract the underlying building blocks or independent components of a data stream, irrespective of the number of discrete channels those components are communicated over. One method to accomplish this task is independent component analysis. The two broadest mathematical definitions of independence as used in ICA are (1) minimization of mutual information between competing nodes and (2) maximization of non-Gaussianity of the output of a single node. The non-Gaussian family of ICA algorithms uses negentropy and kurtosis as mathematical objective functions from which to derive a plasticity rule. To find a plasticity rule capable of ICA we can minimize a kurtosis objective function over the node output activation. The result is ideally the opposite of a peak: a bimodal distribution. That is, we seek a hyperplane that separates the input data into two classes resulting in two distinct positive and negative distributions. Using a kurtosis objective function, it can be shown that a plasticity rule of the following form emerges [11]:

$\Delta {w_i} = {x_i}\left( {\alpha y - \beta {y^3}} \right)$

, where α and β are constants that control the relative contribution of Hebbian and anti-Hebbian plasticity, respectively. The above equation is one form of many that we call the AHaH rule. The important functional characteristics that it shares with all the other forms is that as the magnitude of the post-synaptic activation grows, the weight update transitions from Hebbian to anti-Hebbian learning.

AHaH Attractors as Building Blocks for Machine Learning

An AHaH node is a hyperplane attempting to bisect its input space so as to make a binary decision. There are many hyperplanes to choose from and the question naturally arises as to which one is best. The generally agreed answer to this question is “the one that maximizes the separation (margin) of the two classes.” The idea of maximizing the margin is central to support vector machines, arguably one of the more successful machine learning algorithms. As demonstrated in [11, 12], as well as the results of our PLoS One paper, the attractor states of the AHaH rule coincide with the maximum-margin solution and leads to universal reconfigurable logic and a basis for physically adaptive computation acting on incoming data streams. But we’ll save that for another article!

To learn more about the theory of AHaH computing and how memristive+CMOS circuits can be turned into self-learning computer architecture using the above AHaH rule, continue with our open-access PLOS One paper: AHaH Computing–From Metastable Switches to Attractors to Machine Learning.

References

Turing AM (1952) The chemical basis of morphogenesis. Philosophical Transactions of the Royal Society of London Series B, Biological Sciences 237: 37–72.
Getling AV (1998) Rayleigh-B ́enard Convection: Structures and Dynamics. World Scientific.
Athelogou M, Mert ́e B, Deisz P, Hu ̈bler A, Lu ̈scher E (1989) Extremal properties of dendritic patterns: biological applications. Helvetica Physica Acta 62: 250–253.
Swenson R (1989) Emergent attractors and the law of maximum entropy production: foundations to a theory of general evolution. Systems Research 6: 187–197.
Bejan A (1997) Constructal-theory network of conducting paths for cooling a heat generating volume. International Journal of Heat and Mass Transfer 40: 799–816.
Jorgensen SE, Svirezhev YM (2004) Towards a Thermodynamic Theory for Ecological Systems. Elsevier.
Schneider ED, Sagan D (2005) Into the Cool: Energy Flow, Thermodynamics, and Life. University of Chicago Press.
Lotka AJ (1922) Contribution to the energetics of evolution. Proceedings of the National Academy of Sciences of the United States of America 8: 147–151.
Hatsopoulos GN, Keenan JH (1981) Principles of General Thermodynamics. RE Krieger Publishing Company.
Hebb DO (2002) The Organization of Behavior: A Neuropsychological Theory. Psychology Press.
Nugent A, Kenyon G, Porter R (2004) Unsupervised adaptation to improve fault tolerance of neural network classifiers. In: Proc. 2004 IEEE NASA/DoD Conference on Evolvable Hardware. pp. 146–149.
Nugent MA, Porter R, Kenyon GT (2008) Reliable computing with unreliable components: using separable environments to stabilize long-term information storage. Physica D: Nonlinear Phenomena 237: 1196–1206.