Prerequisites
Introduction
The Memristor Discovery platform is a low cost educational and research tool for exploring memristor electronics. Originally developed as a risk mitigation step in the construction of a memristive learning processor for the Knowm Technology Stack, it has now gone through three generations of refinement. Memristor Discovery provides a minimal complexity platform to investigate individual memristors, memristor synapses and small scale memristor machine learning. All of the code is available open-source on GitHub, making it a great place to start if you need to write a custom experiment to test memristor electronics.
Given the resurgence of interest in Thermodynamic Computing, in this post we are going to make a new Memristor Discovery experiment that will use memristors to solve boolean constraint problems, guiding you through the steps. Before we do this let’s review some relevant material on the problem we are solving, and how we intend to solve it with memristors.
3 Satisfiability Problem (3-SAT)
Boolean satisfiability is a relatively simple to understand problem with a fairly wide range of applicability thanks to the theory of NP-Completeness. The idea is that you have N boolean (binary) variables, lets call them that participate in one or more of M total clauses,
. The clauses are usually written in conjunctive normal form, i.e. an “AND of ORs”:
The goal is to find the boolean values that satisfy the clauses
. As one might expect, if there are not too many clauses the problem is easy and there are usually more than one solution. As the number of clauses increase the difficulty increases until the problem becomes un-satisfiable. Being the first problem that was proven NP-complete, you can imagine there is a lot to say about boolean satisfiability–as well as many advanced computer programs for solving problem instances.
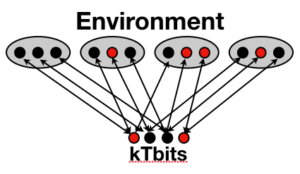
Our solution to the 3-SAT problem can be visualized as below, where the boolean variable values are represented by “kT-Bits”, short for Thermodynamic Bits and the clauses are the “Environment” that provides feedback to the kT-Bits. A kT-bit is a memory device that resolves to a boolean value with a probability that can be modified through positive or negative reinforcement. Stated simply, they are biased random number generators with adjustable biases. A kT-Bit that evaluates true and receives positive feedback will more likely resolve true in the future. A kT-Bit that evaluates true and receives negative feedback will less likely resolve true in the future. If we reward those kT-Bits that satisfy all of their clauses with positive feedback while punishing those kT-Bits that do not satisfy their clauses with negative feedback, the kT-Bits will spontaneously flip-flop until all the clauses are satisfied. It’s not hard to see that the only stationary state is the one where all clauses are satisfied.
Thermodynamic Synapses
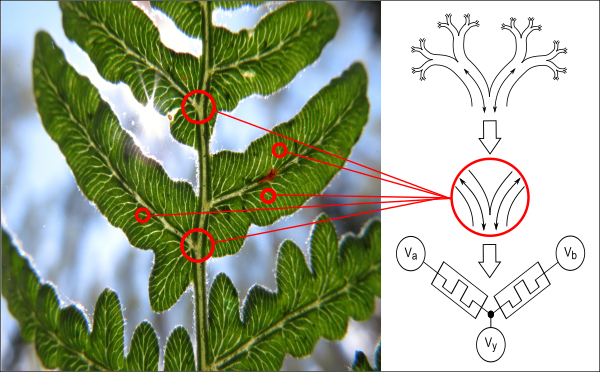
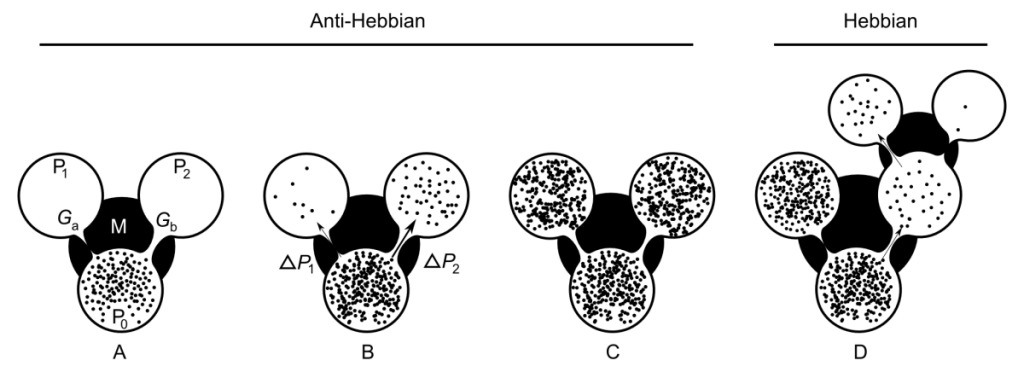
Thermodynamic Synapses are a naturally occurring phenomena that occur anywhere energy is dissipating through competing adaptive channels. Once you know where and how to look, you see they are a building-block for self-organized structures in Nature.
Our work with AHaH Computing was inspired by the simple idea that we can use “artificial thermodynamic synapses” as computational building blocks to solve problems. If we replace “energy dissipating through competing adaptive channels” with “two memristors” we end up with a kT-Synapse. The letters “kT” is a reference to both thermodynamics (Boltzmann’s constant times temperature) and also Knowm Technology (KT). A kT-Synapse is a universal computational building block made possible with the advent of memristor nanotechnology. Like Qubits, they were envisioned many years ago but only recently reduced to practice. Unlike Qubits, they are much more practical as anybody can buy and use them now.
It turns out there are a lot of ways of putting two memristors together, and the four configurations for bipolar memristors are shown below:
kT-Synapses can be used as signed weights in neural networks, ‘probability counters’ in statistical algorithms, reconfigurable logic gates and memory. They are useful little buggers.
Thermodynamic Bits
We can use a kT-Synapse “probabilistic bit generator” aka kT-Bit. The state of the bit is given by the relative conductance of each memristor. We can define “true” to be the condition and “false” to be
. The magnitude of the kT-Bit is a function of the difference in conductance. For the 2-1 configuration above, this is given by:
Any measurement that we perform in the real-world to asses the state of the kT-Bit will be made in the presence of noise ():
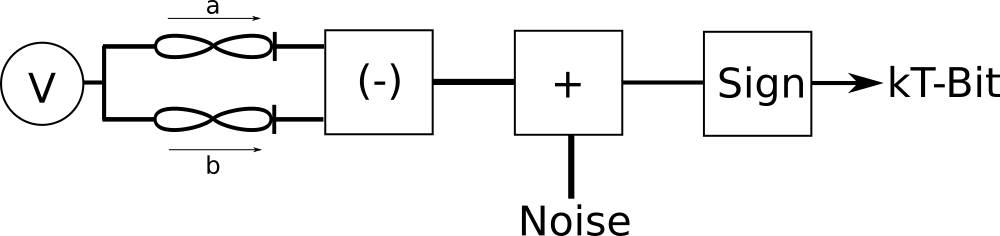
As the evaluation voltage approaches the noise level , the synapse magnitude can be used as a bias to a binary random number generator that is powered by the noise. As an example, in the schematic below we can apply a common voltage to two memristors and measure the differential current in the presence of noise. Taking the sign of the result gives us a boolean value, i.e. our kT-Bit.
A collection of biased random number generators can be used to generate trial solutions to constraint problems. If we have a mechanism to provide feedback to each kT-Synapse, i.e to increment or decrement the relative conducatnce of the memristor pair, then we can ‘focus’ the trial solutions and converge on solutions. In the case of a boolean constraint problem, providing feedback to a kT-Bit is relatively simple: If all the clauses from which a variable participates are satisfied we reinforce its state (make its state more certain) while if a clause is not satisfied we degrade its state (make its state less certain). If it works, keep it. If it does not, change it. If it usually works but suddenly does not work, perhaps change it with a small probability. For this idea to be realized in a circuit we need at least the following.
- kT-Synapse
- Noise source
- Evaluation Logic
The kT-Synapse and the noise source produces a trial kT-bit that is fed into the evaluation logic along with other kT-Bits, one kT-Bit per variable. The evaluation logic implements the clause logic and informs each kT-Synapse if its clauses are satisfied. If they are, the state is reinforced. If they are not, the state is degraded. This is repeat until a solution is found or the user terminates.
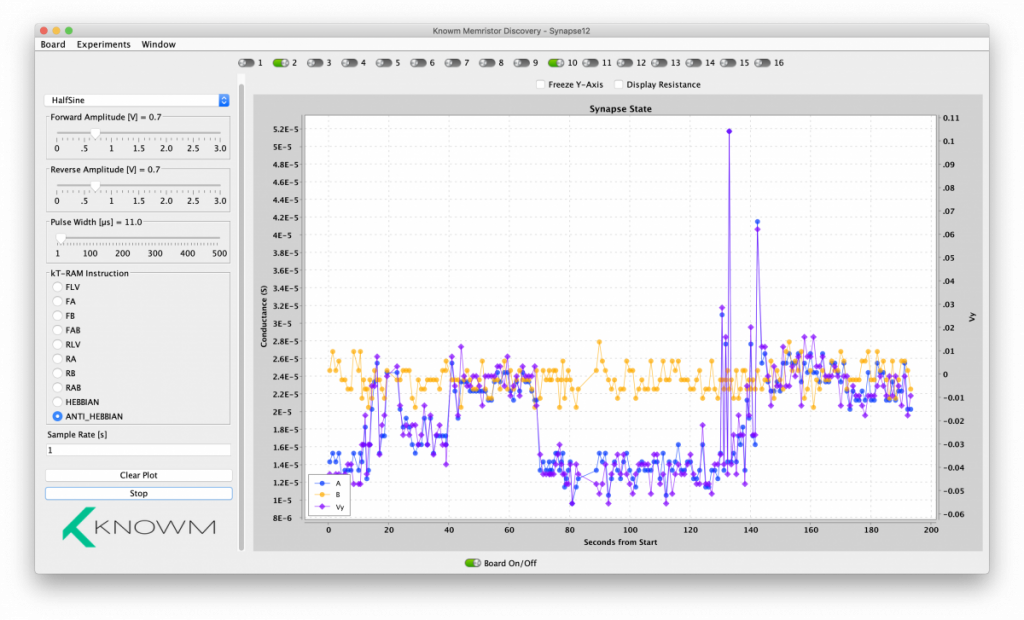
Noise is naturally present in every measurement, which means this is not really anything we have to go to great length to find. We can use the Synapse12 experiment in Memristor Discovery and let it run for a while to see it:
If we can program or “nudge” the conductances of each memristor in a kT-Synapse pair to be approximately the same, the measured state of the synapse should reflect this underlying noise. To do this we will add some new synaptic instructions to the Synapse12 experiment and formalize what we mean by ‘reinforcement’.
If you want to follow along and create your own Memristor Discovery experiment, check out this post for instructions on how to ‘clone’ an existing Memristor Discovery Experiment as a starting point for a new experiment.
Modifying the kT-RAM Controller
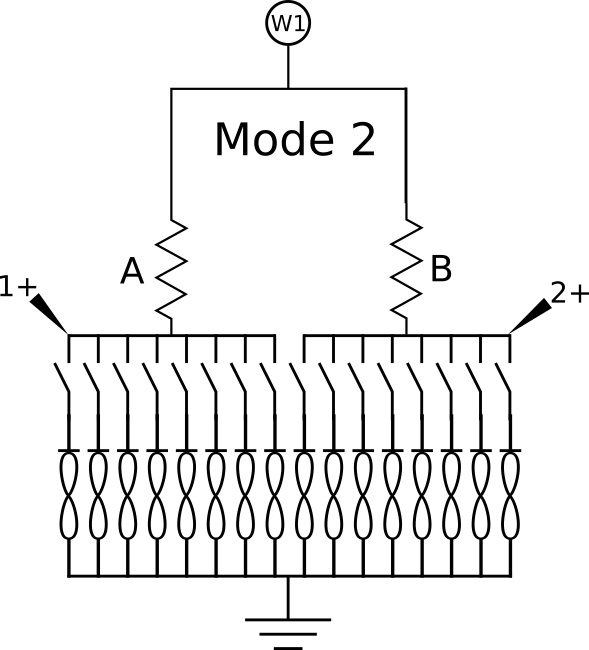
The Synapse12 and Classifier12 experiment in Memristor Discovery has its own version of a kT-RAM controller. kT-RAM is a random-access collection of kT-Synapses. The V2 Memristor Discovery board is a small kT-RAM that uses our 1X16 array memristor chips. Mode 1 is for ‘unitary’ operation, where individual memristors are selected. Mode 2 is for a differential operation, which we are using here. 16 memristors accessed as pairs gives us 8 kt-Bits or one kT-Byte.
We can form a kT-Bit from two memristors picked from the 1-8 and 9-16 sets. We will hard code that kT-Bit 0 is formed from memristors 1 and 9, kT-Bit 1 is formed from memristors 2 and 10, and so on.
The function of the kT-RAM Controller is to associate instructions with voltage drive patterns. Theoretically you can imagine an infinite set of drive patterns but practically it’s best to keep them as simple as possible. The Classifier12 experiment defined only a few simple instructions because that is all that was needed:
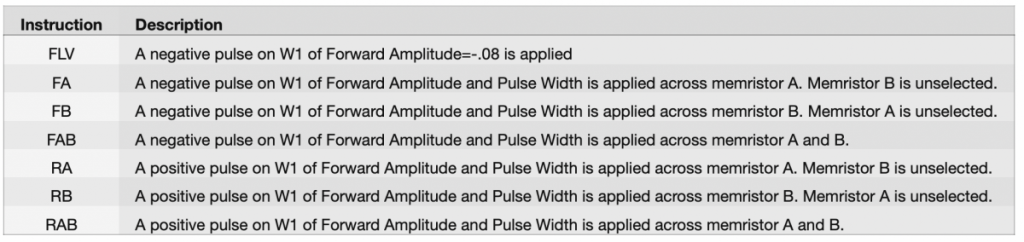
A more practical version of the above instructions is given below, where we simply take stock of how the instruction modifies the conductance of the memristors:
| Instruction | Description |
|---|---|
| FLV | kT-Synapse is read with low voltage for minimal disturbance. |
| FA | Memristors A conductance increased. |
| FB | Memristor B conductance increased. |
| FAB | Memristor A and B conductance is increased. |
| RA | Memristors A conductance decreased. |
| RB | Memristor B conductance decreased. |
| RAB | Memristor A and B conductance decreased. |
To build a kT-Bit we need two instructions that will result in positive and negative feedback to the kT-Bit state. If the synapse is positive and we give it positive-feedback, it needs to get more positive and visa versa. Our work with AHaH Computing was based on the observation that positive and negative feedback can be seen as Hebbian and Anti-Hebbian learning within a broader synaptic learning context and reduced to differential-pair memristor circuits.
| Synaptic Plasticity | Description |
|---|---|
| Hebbian | Any modification to the synaptic weight that increases the probability the synaptic state will remain the same upon subsequent measurement. aka “Select the path.” or “Move toward certainty.” or “Positive feedback.” |
| Anti-Hebbian | Any modification to the synaptic weight that reduces the probability the synaptic state will remain the same upon subsequent measurement. aka “Erase the path.” or “Move toward uncertainty” or “Negative feedback” |
While there are many ways to proceed, I will take the path of least cognitive effort and use the existing instructions to create two new ‘compound’ instructions that we will call HEBBIAN and ANTI_HEBBIAN, respectively. These two instructions will use the memristor conductance values as measured by a proceeding FLV instruction and then execute the appropriate instructions to drive the memristor conductances appropriately.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
public void executeInstruction(SupervisedPattern spikePattern, Instruction instruction) { this.spikePattern = spikePattern; if (instruction == Instruction.HEBBIAN) { if (ga >= gb) {//state is positive. make more positive. execute(Instruction.FA);//increase conductance of A execute(Instruction.RB);//decrease conductance of B } else if (ga < gb) {//state is negative. make more negative. execute(Instruction.RA);//decrease conductance of A execute(Instruction.FB);//increase conductance of B } } else if (instruction == Instruction.ANTI_HEBBIAN) { if (ga >= gb) {//state is positive. Make less positive. execute(Instruction.RA);//decrease conductance of A execute(Instruction.FB);//increase conductance of B } else if (ga < gb) {//state is negative. make less negative. execute(Instruction.FA);//increase conductance of A execute(Instruction.RB);//decrease conductance of B } } else { execute(instruction); } } |
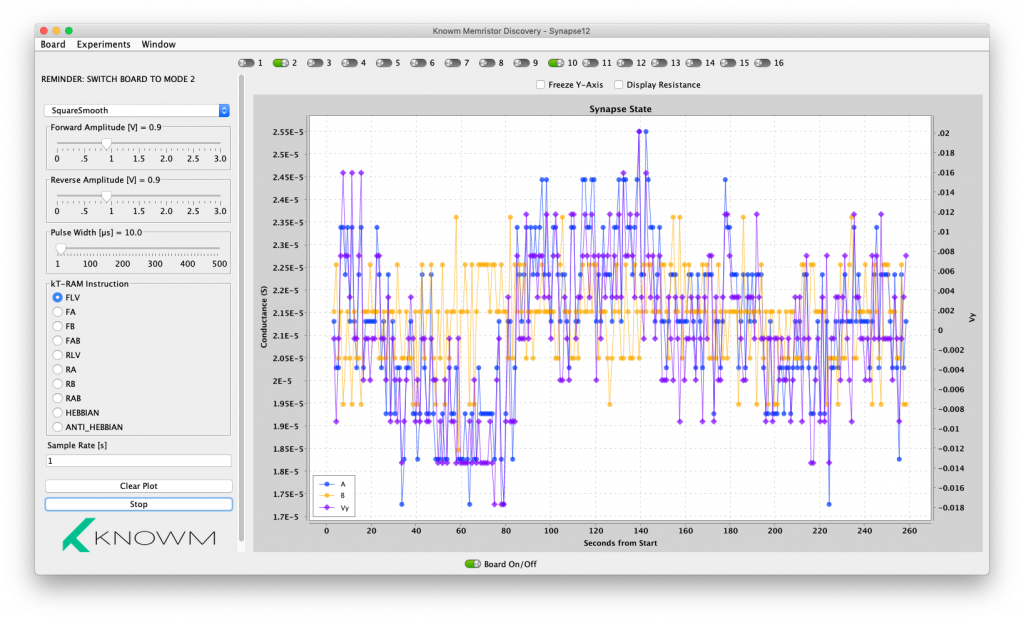
That’s really all we need to do at the hardware level, but we should at least test out our instructions to make sure they have the intended effect before working on the GUI and solving a 3-SAT instance. To test this out I added the HEBBIAN and ANTI_HEBBIAN instructions to the existing Synapse12 experiment and gave it a trial run with a kT-Bit formed from memristor 1 and 9 on a tungsten 1X16 array.
From t=0 to 28s I let the program take measurements with repeated FLV instructions to get a read on the initial state. Memristor A conductance (blue, left vertical scale) is larger than memristor B conductance (orange) and thus the memristor state (purple, right vertical scale) is positive (Vy=.06). From t=28s to t=45s I executed the HEBBIAN instruction. As expected, the synaptic state became more positive as the conductance of memristor B falls and the conductance of memristor A rises. From t=45s to t=76s I executed the ANTI_HEBBIAN instruction and the result was a ‘stochastic oscillation’ of the state. From t=76s I executed the HEBBIAN instruction. Because the state flipped from positive to negative during the ANTI_HEBBIAN instruction, execution of the HEBBIAN instruction causes the state to be reinforced and hence it becomes more negative.
If the amount of force applied (voltage-time product) to change the memristors is large, the ANTI_HEBBIAN instruction will cause oscillations as the kT-Bit flip-flops back and forth. As the force is lowered, via the applied voltage and pulse width, the change in the conductance will be gradual and allow us to move the kT-Synapse state into and out of the noise level more carefully. This can be seen below where we have lowered the applied voltage to .7V and the pulse width to 11us. From t=0 to 40s we execute the ANTI_HEBBIAN instruction to equilibrate the synapse. From t=70 to 80 we execute the HEBBIAN instruction. From t=130s to t=150s we again executed the ANTI_HEBBIAN instruction to remove the bias.
In practice we should be able to solve a 3SAT instance so long as the response to the ANTI-HEBBIAN instruction is not purely oscillatory.
Building a kT-Bit Sat Solver Experiment
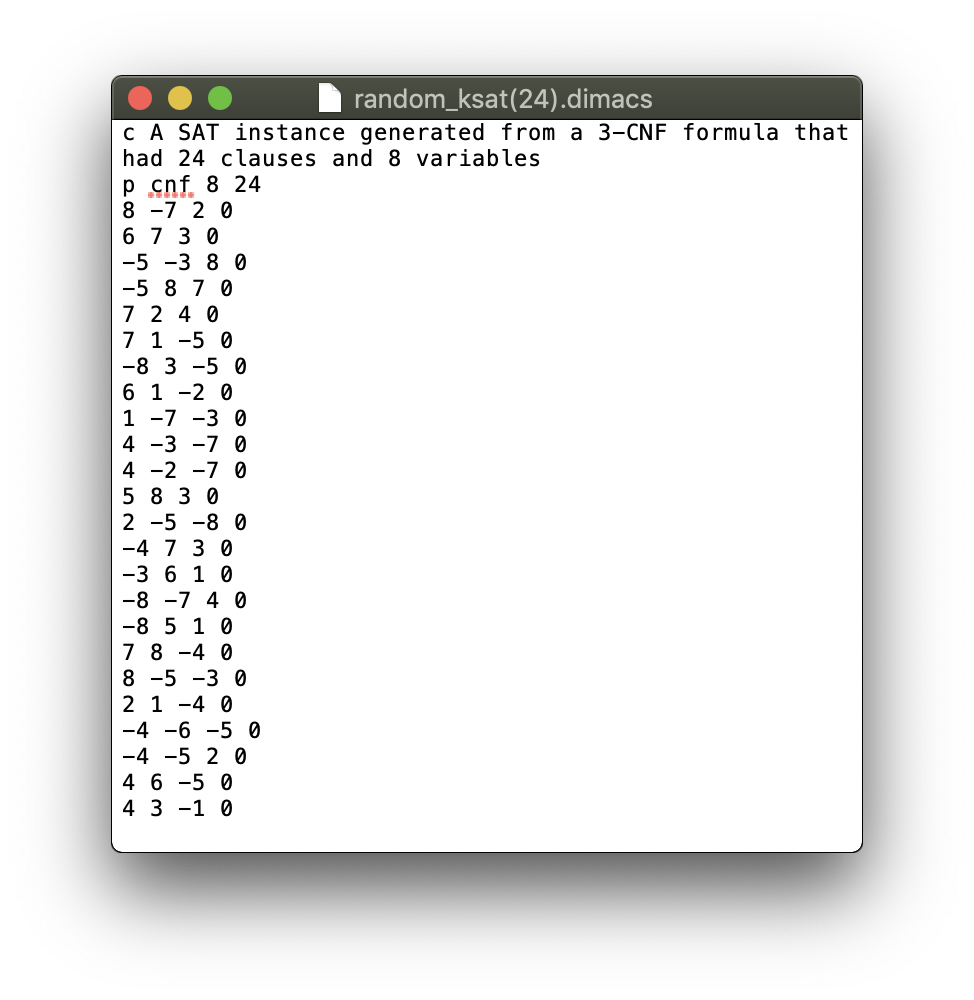
Using the Classifier12 Experiment as a starting point we will clone the experiment and make some modifications for our 3-SAT solver. The top plot that kept track of the classification accuracy can be used to keep track of the number of clauses that are satisfied. The lower plot can be kept the same, since it’s just measuring the state of each kT-Synapse. To generate a 3-SAT problem instance we will use this website, which lets you download files that specify a k-SAT problem instance that looks like this:
The relevant code for the solver is very simple. First we read the state of each synapse with the FLV instruction to minimize disturbance:
The sign of the read values (negative=false, positive-true) are used to to evaluate if they satisfy the constraint problem. The clauses each variable participates in are checked. If all the clauses for a variable are satisfied, feedback is HEBBIAN otherwise it is ANTI_HEBBIAN.
I additionally added a button that will ‘initialize’ the synapses into higher conductance values by alternating the FAB and ANTI_HEBBIAN instructions. This does not really seem to be necessary.
Results and Discussion
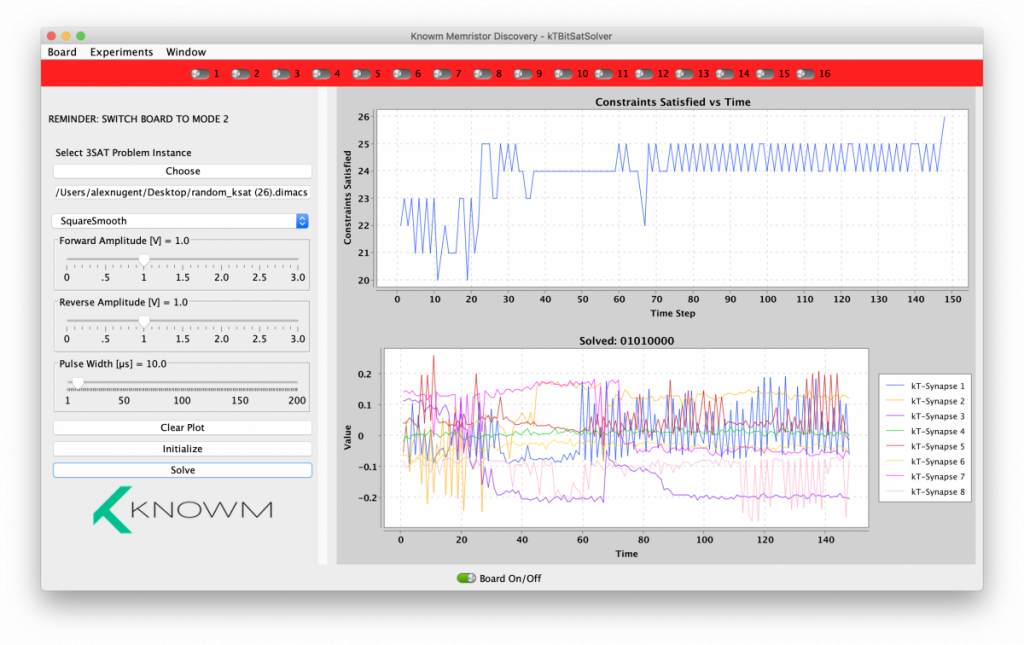
A typical run looks like the following. Rather than go on in detail I encourage you to run the experiment for yourself.
As I increase the number of clauses it has a harder time finding a solution, which is expected. There is no memory or ‘clause learning’ in this solver, which in general is not a good thing but of course not really possible if you only have 16 memristors to play with. For only 8 variables it would be a trivial matter to iterate through all the possible combinations and check to see if a solution exist. As the number of variables grows this becomes a poor strategy quickly and having a dedicated hardware solver may be useful. We could, in principle, reduce the clause evaluation logic to memristor circuits. I suspect that the majority of the energy expended in finding a solution would be spent communicating the kT-Bit binary state to the clause evaluation logic and then communicating the feedback signal back to the kT-bits. Since this sort of solver could in principle be distributed, one could imagine a semi-homogenous fabric where the location of clause logic is ‘compiled’ to be as close to the kT-Bits as possible.
While the endurance of Knowm memristors is over a billion cycles (this is very good for a non-volatile memory element), if the circuit in question is meant to do nothing but flip state constantly then it will undeniably fail after a short time if implemented in a truly scaled-up VLSI manner and run at high frequencies. Another approach could be to use the memristors as tunable analog trimmers and accumulation of charge on an internal capacitor as a mechanism to keep track of feedback. This approach could use the adaptive nature of memristors to compensate for the variable of the CMOS while using the high switching endurance of CMOS to generate candidate solution. Since the clause logic remains constant over a problem instance, this could easily be implemented in a reconfigurable memristor logic fabric.





















Leave a Comment