Reinforcement Learning

Reinforcement Learning

Learning by interacting with our environment is perhaps the first form of learning that capable organisms discovered during the beginning of intelligence. Among the first examples were simple celled organisms that exercised the connection between light and food to gain information, about the consequences of actions, and about what to do in order to achieve goals [1].

The same is true for humans as well. Whether we are learning to drive a car or to hold a conversation, we are acutely aware of how our environment responds to what we do, and we seek to build strategies for maximizing our reward.

This type of learning is called Reinforcement Learning and it is used in the field of artificial intelligence and Machine Learning to train decision-making agents. Notably robots that can return table tennis balls [2], fly helicopters [3], and play ATARI video games [4], or bots that can execute trades on the stock market [5], perform complex combinatorial optimizations [6] and clean up software [7].

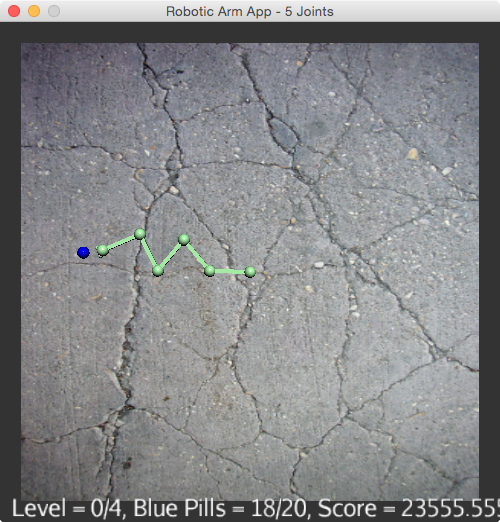
Knowm API – Robotic Arm

Reinforcement Learning Framework

In all cases, we can describe a Reinforcement learning task as one in which an agent interacts with an environment, in a sequence of actions, observations and rewards. The goal of the agent, in this description, is to interact with the environment by selecting actions in a way that maximizes its expected value of future rewards. In other words, we want to choose the actions which have the highest action-value or Q*(a,s).

The true action-value function Q*(a,s) is unknown to a learner. Thus the basic goal behind reinforcement learning algorithms is finding a Q(a,s) which is close as possible to Q*(a,s) [4].

If our decision processes is finite and has a tractable number of states, Q*(a,s) can be directly solved with Dynamic Programming methods such as value-iteration and policy-iteration [7]. It is often the case however, that the state space of a decision problem is either infinite or exponentially large (in most robotics problems for instance) and solving directly for Q*(a,s) is an unreasonable endeavor. Under these conditions, the learner must approximate Q*(a,s) with Q(a,s).

Any type of function approximator can be used for this task – including linear , polynomial, and Neural Network approximators [8].

Image by iwannt

Training the Approximator Q(a,s)

If samples could be drawn directly from Q*(a,s) then training a function approximator could be accomplished in the same way as any other supervised learning task. Unfortunately, Q*(a,s) is inherently difficult to measure, especially when rewards are achieved over long sequences of actions or in partially stochastic environments [7]. Did going to sleep early last night really help me ace that test today?

In practice, statistical methods are used for calculating the value of Q*(a,s) by taking the rewards gained during a trial and attributing this to the actions taken, often discounted so that earlier actions receive less value [8]. The actual method for averaging rewards depends on implementation. Of note, are direct Monte Carlo averages, variations of Temporal Difference Methods and Q and R learning [9].

Once approximate samples, S(a,s) ~= Q*(a,s), are created, the actual training of Q*(a,s) will depend on the type of function approximator used. Artificial Neural Networks, for instance, can use gradient descent to minimize the error between a S(a,s) and Q(a,s) [9]. Linear approximators can be trained through interpolation or other Machine Learning method.

Generating Sample Experience

The way samples are generated by the learner is another important aspect of an RL method. The state space is often too large to explore exhaustively, instead a transition policy must be found which will traverse useful sequences. In practice, the transition policy follows closely along actions which have a high value. This may change continually as more information is gained ( on-policy search ) or be selected randomly from a behavior distribution ( off policy search ) [7].

A number of hurdles arise in both cases. For one, the learner must be able to generalize its approximation of Q*(a,s) across untrained regions of space. A difficult task if actions can cause large effects in future value. Additionally, a trade-off arises between exploration and exploitation during simulation: If the learning always exploits a high-value path, it may learn an optimal strategy quickly but a more optimal path may go unseen and if exploration is applied exclusively, a good strategy may never emerge [7]. The discovery of the high-jumping Fosbury Flop is an example of this.

Image by Steven Pisano

Reinforcement Learning on kT-RAM

We can extend traditional methods of Reinforcement Learning to use a neuromorphic chip like kT-RAM by building our agents decision-making system with a collection of AHaH nodes. These can be trained using Hebbian feedback as we gather experience from the environment. In this model, Anti-Hebbian and Hebbian feedback acts as a binary good/bad reward signal for our learner. We can buffer previous actions and apply these to multistep sequences of arbitrary length.

An on-policy search method may also be incorporated by using the output of these AHaH nodes during simulation, or, conversely, a higher order procedure can be built which uses the AHaH collectives output to dictate the search policy.

In the article following this one, we demonstrate a proof of concept example of this. Here we apply a collection of AHaH nodes to control a robotic arm in a motor control task.

Image by Dan Ruscoe

Conclusion

One way of thinking about Reinforcement Learning is as a method of learning how to act towards reaching a goal in a decision task. This is a broad type of learning which encapsulates, in a large part, what we would expect an intelligent agent to be capable of. It makes sense then, that natural problems arise, the trade-off between exploration and exploitation, the need to generalize, the ambiguity of attributing value to action, all of which have parallels in our own experience.

We can describe RL problems using a canonical framework based on states, transitions, rewards, and value. This allows us to design statistical and Machine Learning methods for finding intelligent decision-making agents. This has been shown to work for a number of complex tasks.

Additionally, we can use this model to design a Reinforcement Learner using kT-RAM. This is an interesting result for a number of reasons. Primarily, the usual improvements in terms of energy consumption and speed realized by a physical chip are likely to greatly benefit RL in its current state. Looking forward however, we may also find it appealing that a physical system like this, which strictly uses the Hebbian learning rules seen in our own brain and in nature, could be actualized for Reinforcement Learning.

Further Reading

TOC: Table of Contents
Previous: Complex Sine Wave Example
Next: Robotic Arm Motor Control

References

1. Tagkopoulos, I., Liu, Y.-C. & Tavazoie, S. Science advanced online publication, doi:10.1126/science.1154456 (2008).

2. Peters, Jan, and Stefan Schaal. “Reinforcement learning of motor skills with policy gradients.” Neural networks 21.4 (2008): 682-697.

3. Ng, Andrew Y., et al. “Autonomous inverted helicopter flight via reinforcement learning.” Experimental Robotics IX. Springer Berlin Heidelberg, 2006. 363-372.

4. Mnih, Volodymyr, et al. “Playing atari with deep reinforcement learning.” arXiv preprint arXiv:1312.5602 (2013).

5. Moody, John, et al. “Performance functions and reinforcement learning for trading systems and portfolios.” Journal of Forecasting 17.56 (1998): 441-470.

6. Dorigo, Marco, and L. M. Gambardella. “Ant-Q: A reinforcement learning approach to the traveling salesman problem.” Proceedings of ML-95, Twelfth Intern. Conf. on Machine Learning. 2014.

7. Sutton, Richard S., and Andrew G. Barto. Reinforcement learning: An introduction. Vol. 1. No. 1. Cambridge: MIT press, 1998.

8. Boyan, Justin, and Andrew W. Moore. “Generalization in reinforcement learning: Safely approximating the value function.” Advances in neural information processing systems (1995): 369-376.

9. Tesauro, Gerald. “Temporal difference learning and TD-Gammon.” Communications of the ACM 38.3 (1995): 58-68.