Knowm Memristors
Purchase memristors at www.knowm.com.
Knowm memristor research die
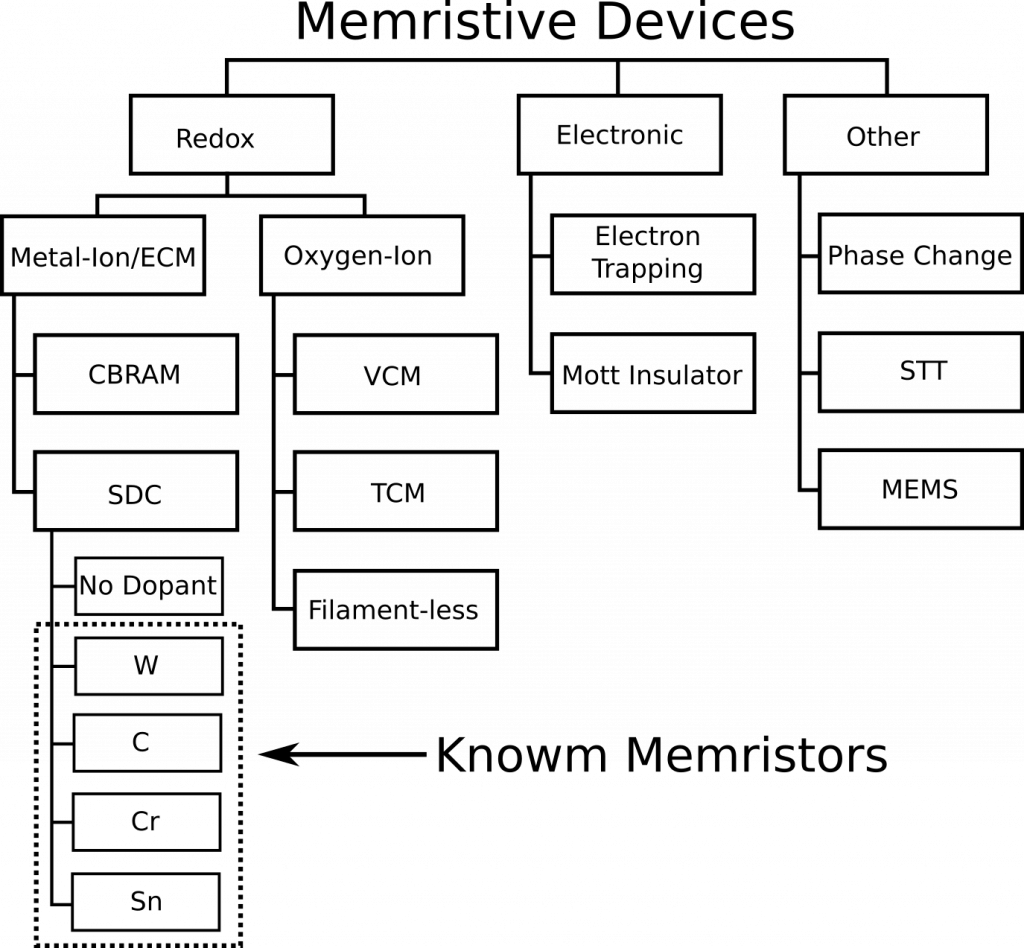
It was originally thought that metal-ion memristors could not hold analog state information (and suffered other problems), but this was turned on its head with the SDC memristor. While traditional metal-ion devices form (grow) metallic ‘filaments’ between electrodes, SDC devices constrain the movement of ions to a chemically created channel structure. Think of it like ‘cracked glass’, where M-ions move in the cracks between the electrode. The channels provide support for conductive pathways, while the addition of M-ions into the channels raises or lowers the conductance. The result is a much more consistent and stable device. SDC memristors are distinct from, and superior to, Conductive Bridge RAM (CBRAM) technology and represent their own new class of memristor.
Memristor Taxonomy
The first time a device is operated after fabrication the self-directed channel is formed during application of a positive potential to the top electrode. The potential required for this operation is typically the same as required during normal device operation. This first operation generates Sn ions from the SnSe layer and forces them into the ‘active’ Ge2Se3 layer, where they undergo a chemical reaction. During this reaction, the glass network is distorted to provide conductive channels for the movement of Ag+ during device operation. The resistance is tunable in the lower and higher directions by movement of Ag into or away from these channels through application of either a positive or negative potential, respectively, across the device. Knowm memristor are Ag+ ion SDC memristor where the active layer has been doped to enhance/optimize the memristors properties. Knowm Memristors currently come in four variants, dependent on the dopant: W, C, Sn and Cr.
Memristor Comparison
Additional Resources
Purchase memristors at www.knowm.com.